Pengertian
Matriks adalah sekumpulan bilangan yang disusun secara baris dan kolom dan ditempatkan pada kurung biasa atau kurung siku. Bilangan-bilangan yang terdapat di suatu matriks disebut dengan elemen atau anggota matriks. Dengan representasi matriks, perhitungan dapat dilakukan dengan lebih terstruktur. Pemanfaatannya misalnya dalam menjelaskan persamaan linier, transformasi koordinat, dan lainnya. Matriks seperti halnya variabel biasa dapat dimanipulasi, seperti dikalikan, dijumlah, dikurangkan dan didekomposisikan.
Penjumlahan Matriks
Dua matriks dapat dijumlahkan apabila kedua matriks tersebut memiliki ordo yang sama. Matriks hasil penjumlahannya juga akan memiliki ordo yang sama dengan matriks yang dijumlahkan. Komponen-komponen matriks hasil penjumlahan diperoleh dengan cara menjumlahkan komponen-komponen setiap matriks yang seletak. Coba perhatikan penjumlahan dua matriks berordo 2 x 2 berikut ini.
 Pada penjumlahan matriks di samping, masing-masing matriks yang dijumlahkan sama-sama berordo 2 x 2 dan hasil penjumlahannya juga berordo 2 x 2 sama dengan ordo matriks yang dijumlahkan. Komponen baris1-kolom1 diperoleh dengan cara menjumlahkan baris1-kolom1 pada matriks pertama (yaitu a) dan komponen baris1-kolom1 pada matriks kedua (yaitu e), dan seterusnya.
Pada penjumlahan matriks di samping, masing-masing matriks yang dijumlahkan sama-sama berordo 2 x 2 dan hasil penjumlahannya juga berordo 2 x 2 sama dengan ordo matriks yang dijumlahkan. Komponen baris1-kolom1 diperoleh dengan cara menjumlahkan baris1-kolom1 pada matriks pertama (yaitu a) dan komponen baris1-kolom1 pada matriks kedua (yaitu e), dan seterusnya.Pengurangan Matriks
Pengurangan matriks A oleh matriks B, ditulis A - B adalah penjumlahan matriks A dengan lawan dari matriks B, yaitu (-B). Konsep pengurangan matriks ini sama dengan penjumlahan matriks. Syarat pada penjumlahan matriks berlaku juga untuk pengurangan matriks. Perhatikan contoh pengurangan matriks berikut ini.
Sifat-Sifat Penjumlahan dan Pengurangan Matriks
Untuk setiap matriks A, B, dan C yang berordo sama berlaku:
1. A + B = B + A (sifat komutatif)
2.A + (B + C) = (A + B) + C (sifat asosiatif)
3.A + O = O + A = A (sifat matriks nol/identitas)
4.A + B = O ↔ B = -A
5.A - B = A + (-B)
Perkalian Matriks
Operasi perkalian matriks berbeda dengan operasi penjumlahan/pengurangan matriks yang cukup sederhana. Operasi perkalian matriks mempunyai metode tersendiri. Dua matriks dapat dioperasikan dengan perkalian jika banyak kolom matriks pertama sama dengan banyak baris matriks kedua , sedangkan hasil perkalian matriksnya akan memiliki baris yang sama banyak dengan baris matriks pertama dan memiliki kolom yang sama banyak dengan kolom matriks kedua, dapat ditulis sebagai berikut :
Metode perkalian dua matriks adalah memasangkan baris pada matriks pertama dengan kolom pada matriks kedua. Perhatikan metode perkalian matriks berikut ini.
Martiks Invers
Jika A dan B adalah matriks persegi, dan berlaku  maka dikatakan matriks A dan B saling invers. B disebut invers dari A, atau ditulis
maka dikatakan matriks A dan B saling invers. B disebut invers dari A, atau ditulis  . Matriks yang mempunyai invers disebut invertible atau matriks non singular, sedangkan matriks yang tidak mempunyai invers disebut matriks singular.
. Matriks yang mempunyai invers disebut invertible atau matriks non singular, sedangkan matriks yang tidak mempunyai invers disebut matriks singular.
Untuk mencari invers matriks persegi berordo 2×2, coba perhatikan berikut ini :
Jika  dengan
dengan  , maka invers dari matriks A (ditulis
, maka invers dari matriks A (ditulis  ) adalah sebagai berikut:
) adalah sebagai berikut:
Jika  maka matriks tersebut tidak mempunyai invers, atau disebut matriks singular.
maka matriks tersebut tidak mempunyai invers, atau disebut matriks singular.
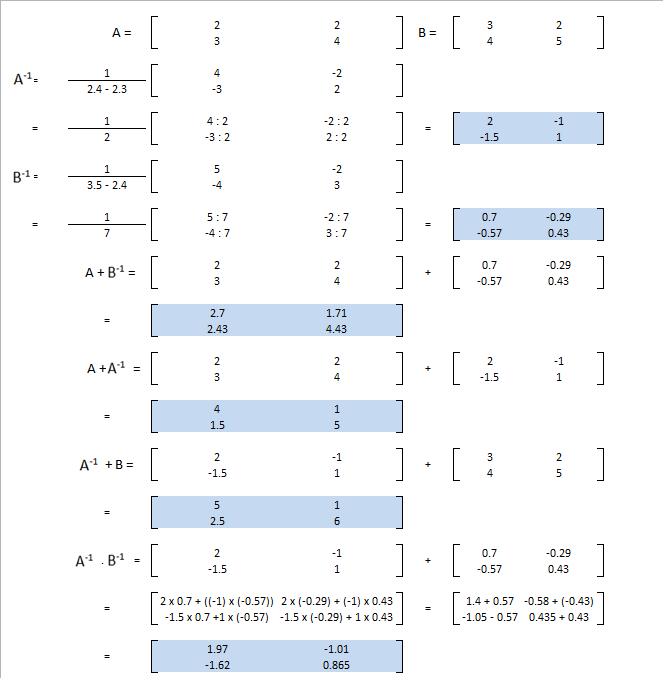
Soal Latihan
Tentukan :
| a. A-1 | e. A-1+B |
| b. B-1 | f. A-1.B-1 |
| c. A+B-1 | g. A.B-1 |
| d. A+A-1 | h. A-1.B |
.png)
.png)


Terimakasih atas informasinya :)
BalasHapus